Pascal's Triangle, an iconic mathematical construct, has fascinated mathematicians, scientists, and scholars for centuries. Its origins can be traced back to ancient civilizations, and it continues to be a valuable tool in various fields of mathematics and science. In this essay, we will embark on a journey through the history of Pascal's Triangle, exploring its evolution and enduring importance.
Ancient Beginnings

Figure 1. Blaise Pascal in a brown coat. Credit: picryl
The history of Pascal's Triangle is a tale that spans millennia. While the specific name "Pascal's Triangle" is attributed to the French mathematician Blaise Pascal, its existence and properties were known long before his time. Ancient Chinese mathematicians, such as Yang Hui and Jia Xian, discovered similar triangular patterns as early as the 13th century.
Blaise Pascal's Contribution
Blaise Pascal, in the 17th century, is often credited with popularizing the triangular arrangement of numbers that bears his name. He documented its properties and applications in his work "Traité du Triangle Arithmétique" (Treatise on the Arithmetical Triangle), published in 1653.
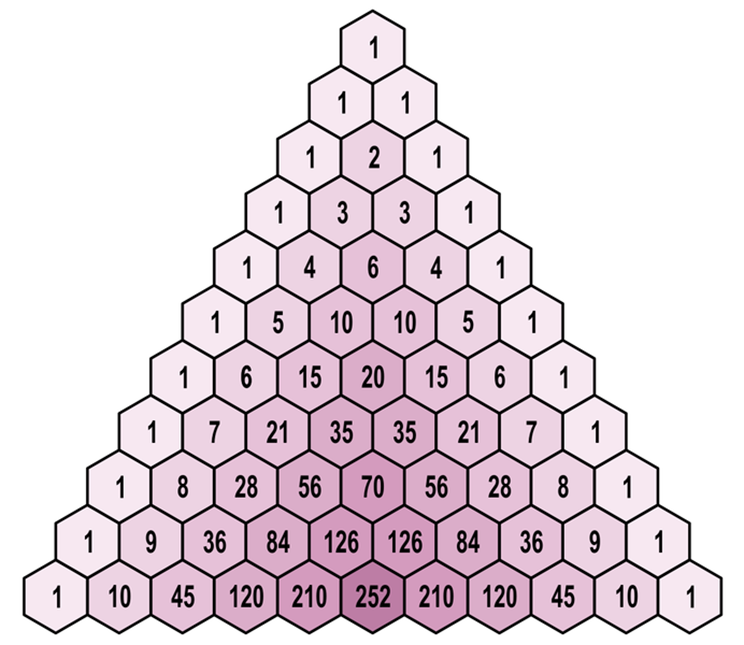
Figure 2. Pascal's Triangle. Credit: WIKIPEDIA
Pascal's Triangle consists of an array of numbers in which each number is the sum of the two numbers directly above it. Starting with a single "1" at the top, each row is generated by adding the adjacent numbers from the previous row. This simple rule gives rise to a surprisingly rich structure of numbers.
Mathematical Significance
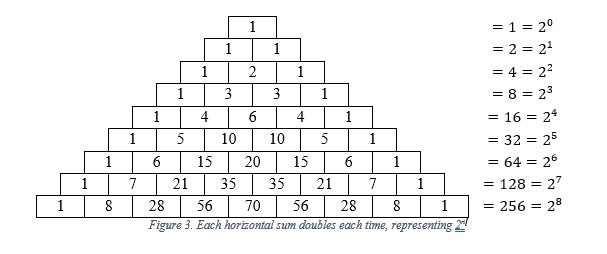
The importance of Pascal's Triangle in mathematics cannot be overstated. It holds a treasure trove of mathematical properties and relationships. Some of its key significance includes:
- Binomial Coefficients: Pascal's Triangle is a visual representation of binomial coefficients. Each number in the triangle corresponds to a coefficient in the expansion of the binomial . This relationship is fundamental in algebra, combinatorics, and probability.
- Combinatorics: The numbers in Pascal's Triangle are used to solve combinatorial problems, such as counting combinations and permutations. They play a critical role in probability theory, statistics, and graph theory.
- Number Patterns: The triangle reveals numerous patterns and sequences, including triangular numbers, Fibonacci numbers, and Catalan numbers. These sequences have applications in a wide range of mathematical and scientific contexts.
- Calculus: Pascal's Triangle has connections to calculus, particularly in the study of calculus of finite differences and numerical methods.
- Geometry: It has geometric implications, such as the distribution of binomial coefficients in different dimensions, which has applications in algebraic geometry.
- Number Theory: The triangle's properties are relevant to various topics in number theory, including congruences and Diophantine equations.
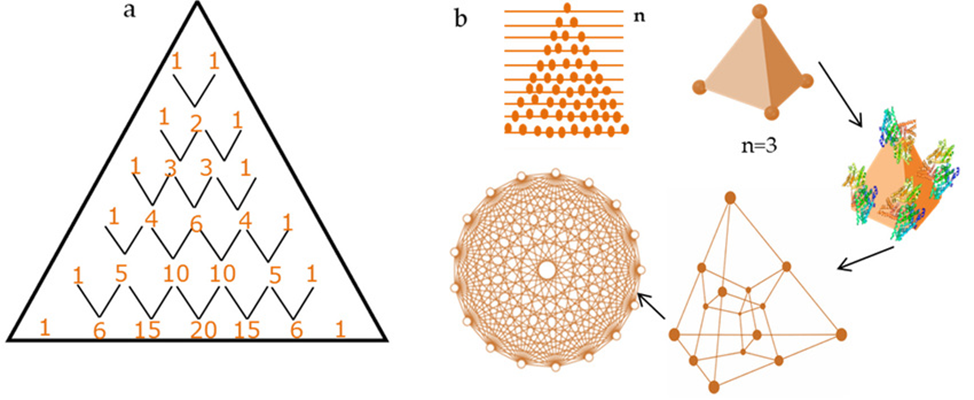
Figure 4. Diagram showing connection of Pascal's triangle to geometric design: (a) illustration of Pascal's Triangle and (b) Sketch of Pascal's triangle and n-simplex when n = 3, representing a tetrahedron structure, when tetrahedron structures join together symmetrically into a 120-cell unit it gives a 2-D projection or symmetric unit which resembles the ring pattern. Credit: Researchgate
Beyond Mathematics
Pascal's Triangle transcends mathematics and finds applications in various fields:
- Physics: It is used in probability distributions, quantum mechanics, and statistical mechanics.
- Computer Science: Pascal's Triangle is employed in algorithms for various applications, including cryptography, data compression, and image processing.
- Art and Design: The triangle's patterns have inspired artists, architects, and designers in creating aesthetically pleasing and mathematically harmonious compositions.
To sum up, Pascal's Triangle is a testament to the timeless beauty and utility of mathematical constructs. Its history, spanning centuries and cultures, underscores its universal appeal. From its ancient origins to its modern applications, this mathematical gem continues to enrich our understanding of the world and remains an enduring symbol of the elegance and power of mathematics.
References
- Pascal, Blaise, "Treatise on the Arithmetical Triangle" (1952). 2023, September 22-23, ORESME Reading Group Meeting. 1. https://www.exhibit.xavier.edu/oresme_2023sept/1
- Bernardo, M. M., & Untalan, J. C. (1991). Pascal's triangle: Properties and applications. Retrieved from https://animorepository.dlsu.edu.ph/etd_bachelors/15948
- A. Starkov, “Fractal properties of binary matrices constructed using the generalized Pascal's triangle and applications”, Algebra, Geometry, and Combinatorics, Itogi Nauki i Tekhniki. Ser. Sovrem. Mat. Pril. Temat. Obz., 214, VINITI, Moscow, 2022, 69–75.
- Pascal’s Triangle https://www.mathsisfun.com/pascals-triangle.html
- Self-Assembly of Human Serum Albumin: A Simplex Phenomenon - Scientific Figure on ResearchGate. Available from: https://www.researchgate.net/figure/Diagram-showing-connection-of-Pascals-triangle-to-geometric-design-a-illustration-of_fig2_319946363/actions [accessed 29 Sep, 2023]
Prepared by,
Dr. Mohd Ezad Hafidz Hafidzuddin
Mathematics Division
Date of Input: 03/10/2023 | Updated: 03/10/2023 | hasniah
MEDIA SHARING